142. Linked List Cycle II

• Link: https://leetcode.com/problems/linked-list-cycle-ii/

Question

Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.

Do not modify the linked list.

Example 1:

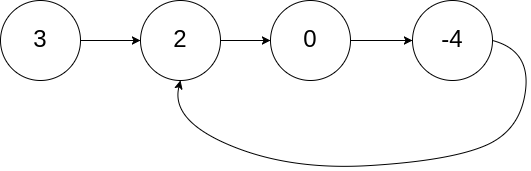
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

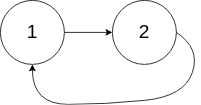
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Constraints:

• The number of the nodes in the list is in the range [0, 104].
• -105 <= Node.val <= 105
• pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

Approach 1: Brute Force

• Using unordered_map data structure

Algorithm

1. Declare unordered_map<ListNode*, int> m
2. Declare & initialize a curr node to head
3. Loop through the linkedlist using curr
   1. if curr exists in the map m return curr
   2. Add curr to the map.
   3. curr = curr->next
4. Return NULL.

Code

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        unordered_map<ListNode*, int> m;

        ListNode* curr = head;

        while(curr) {
            if (m.find(curr) != m.end()) return curr;
            m[curr]++;
            curr = curr->next;
        }

        return NULL;
    }
};

Complexity Analysis

• Time Complexity: $O(N)$
• Space Complexity: $O(N)$

Approach 2: Optimal

• Floyd's tortoise hare algorithm

Algorithm

1. Declare & initialize ListNode* fast & ListNode* slow to head.
2. Loop through the LL till fast && fast->next exists
   1. Increment fast 2 nodes at a time.
   2. Increment slow 1 node at a time.
   3. If fast == slow
      1. Reinitialize slow to head
      2. Loop through the LL till slow != fast
         1. Increment fast 1 node at a time
         2. Increment slow 1 node at a time
      3. Return slow
3. Return NULL

Code

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;

        while(fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) {
                slow = head;
                while (fast != slow) {
                    fast = fast->next;
                    slow = slow->next;
                }
                return slow;
            }
        }

        return nullptr;
    }
};

Complexity Analysis

• Time Complexity: $O(N)$
• Space Complexity: $O(1)$