1462. Course Schedule IV

#leetcode #dsa/graphs #dsa/dp

Question

There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course ai first if you want to take course bi.

Prerequisites can also be indirect. If course a is a prerequisite of course b, and course b is a prerequisite of course c, then course a is a prerequisite of course c.

You are also given an array queries where queries[j] = [uj, vj]. For the jth query, you should answer whether course uj is a prerequisite of course vj or not.

Return a boolean array answer, where answer[j] is the answer to the jth query.

Example 1:

Input: numCourses = 2, prerequisites = 1,0, queries = [[0,1],[1,0|0,1],[1,0]]
Output: [false,true]
Explanation: The pair [1, 0] indicates that you have to take course 1 before you can take course 0.
Course 0 is not a prerequisite of course 1, but the opposite is true.

Example 2:

Input: numCourses = 2, prerequisites = [], queries = [[1,0],[0,1|1,0],[0,1]]
Output: [false,false]
Explanation: There are no prerequisites, and each course is independent.

Example 3:

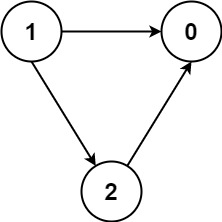
Input: numCourses = 3, prerequisites = [[1,2],[1,0],[2,0|1,2],[1,0],[2,0]], queries = [[1,0],[1,2|1,0],[1,2]]
Output: [true,true]

Constraints:

Approach 1: Brute Force

Intuition

Algorithm

  1. Build graph & indegree
    • Convert prerequisites to adjacency list.
    • Compute indegree of each node.
  2. Topological sort (Kahn’s algorithm)
    • Push all nodes with indegree = 0 into a queue.
  3. DP propagation using topo order
    • Create a boolean table table[n][n] initialized to false.
    • While queue is not empty:
      • Pop curr
      • For each neighbor of curr:
        1. Mark table[curr][neighbor] = true (direct prerequisite)
        2. For all i:
          • If i is a prerequisite of curr (table[i][curr] == true)
          • Then mark i as a prerequisite of neighbor
            → table[i][neighbor] = true
        3. Decrement indegree of neighbor; if it becomes zero, push it to queue.
  4. Answer the queries
    • For each query (u, v), return table[u][v].

Code

class Solution {
public:
    vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
        
        // Build adjacency list and indegree array for Kahn's topological sort.
        vector<vector<int>> adj(n);
        vector<int> indegree(n, 0);

        for (auto &edge : prerequisites) {
            int u = edge[0];
            int v = edge[1];

            adj[u].push_back(v);   // directed edge u -> v
            indegree[v]++;         // v depends on u
        }

        // Push all nodes with indegree = 0 into queue (starting points of topo sort).
        queue<int> q;
        for (int i = 0; i < n; i++) {
            if (indegree[i] == 0) {
                q.push(i);
            }
        }

        // table[u][v] = true means:
        //     "u is a prerequisite (direct or indirect) of v"
        vector<vector<bool>> table(n, vector<bool>(n, false));

        // Process nodes in topological order.
        while (!q.empty()) {
            int curr = q.front();
            q.pop();

            // Traverse all neighbors of 'curr'
            for (int neighbor : adj[curr]) {

                // Direct edge: curr is a prerequisite of neighbor
                table[curr][neighbor] = true;

                // Propagate prerequisites:
                // For every course i that is a prerequisite of curr,
                // i must also be a prerequisite of neighbor.
                //
                // If i -> ... -> curr AND curr -> neighbor,
                // then i -> ... -> neighbor.
                for (int i = 0; i < n; i++) {
                    if (table[i][curr]) {
                        table[i][neighbor] = true;
                    }
                }

                // Standard Kahn's topo decrease indegree
                indegree[neighbor]--;
                if (indegree[neighbor] == 0) {
                    q.push(neighbor);
                }
            }
        }

        // Answer queries using the computed table.
        vector<bool> answers(queries.size());
        for (int i = 0; i < queries.size(); i++) {
            int u = queries[i][0];
            int v = queries[i][1];

            // True if u is a direct or indirect prerequisite of v
            answers[i] = table[u][v];
        }

        return answers;
    }
};

Complexity Analysis