1631. Path With Minimum Effort

#leetcode #dsa/graphs #dsa/graphs/shortest-path

Question

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1:

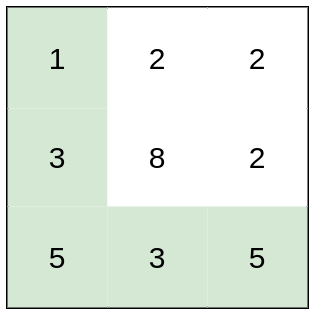
Input: heights = [[1,2,2],[3,8,2],[5,3,5|1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

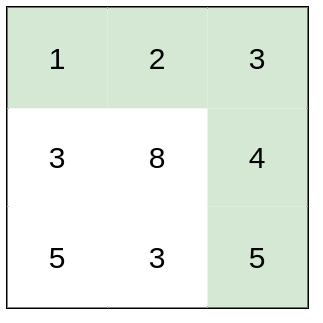
Input: heights = [[1,2,3],[3,8,4],[5,3,5|1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

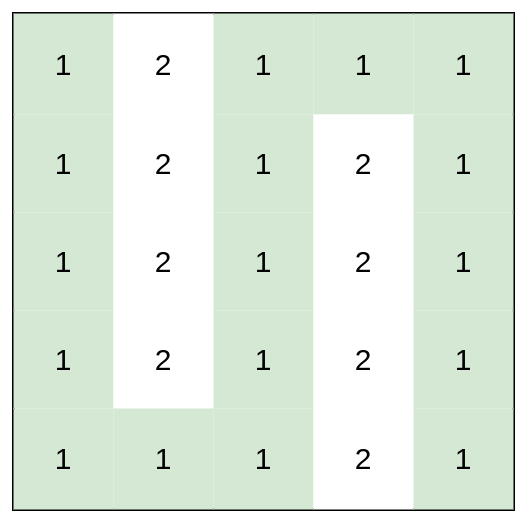
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1|1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

Constraints:

Approach 1: Brute Force

Intuition

Algorithm

  1. Convert heights grid to adj matrix
  2. Dijkstra's algorithm, instead of addition of weights we are just getting the max of the new distance and current distance

Code

class Solution {
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        // 0. convert adj matric to adj list
        vector<vector<int>> directions = {
            {-1, 0}, 
            {0, -1},
            {1, 0},
            {0, 1}
        };
        auto hash_pair = [](const std::pair<int, int>& p) {
            return std::hash<int>{}(p.first) ^ std::hash<int>{}(p.second);
        };

        int rows = heights.size(), cols = heights[0].size();
        unordered_map<pair<int, int>, vector<pair<pair<int, int>,int>>, decltype(hash_pair)> adj;
        for (int i = 0 ; i < rows ; i++) {
            for (int j = 0 ; j < cols ; j++) {
                int r = i;
                int c = j;

                if (adj.find({r, c}) == adj.end()) {
                    adj[{r, c}] = {};
                }

                for (auto& direction: directions) {
                    int nr = r + direction[0];
                    int nc = c + direction[1];

                    if (nr < 0 || nr >= rows || nc < 0 || nc >= cols ) {
                        continue;
                    }
                    int absDiff = abs(heights[r][c] - heights[nr][nc]);

                    adj[{r, c}].push_back({{nr, nc}, absDiff});
                }         
            }
        }


        // 1. dijkstra
        priority_queue<
            pair<int, pair<int,int>>,
            vector<pair<int, pair<int,int>>>,
            greater<pair<int, pair<int,int>>>
        > pq;


        unordered_map<pair<int, int>, int, decltype(hash_pair)> dist;

        for (int i = 0 ; i < rows ; i++) {
            for (int j = 0 ; j < cols ; j++) {
                dist[{i, j}] = INT_MAX;
            }
        }

        pq.push({0, {0, 0}});
        dist[{0, 0}] = 0;

        while(!pq.empty()) {
            auto node = pq.top().second;
            auto currDist = pq.top().first;
            pq.pop();

            for (auto it: adj[node]) {
                auto neighbor = it.first;
                auto weight = it.second;

                int newDist = max(currDist, weight);

                if (newDist < dist[neighbor]) {
                    dist[neighbor] = newDist;
                    pq.push({newDist, neighbor});
                }
            }
        }

        return dist[{rows - 1, cols - 1}];
    }
};

Complexity Analysis

Approach 2: Better

Intuition

Algorithm

Code

Complexity Analysis

Approach 3: Optimal

Intuition

Algorithm

Code

Complexity Analysis