2192. All Ancestors of a Node in a Directed Acyclic Graph

• Link: https://leetcode.com/problems/all-ancestors-of-a-node-in-a-directed-acyclic-graph/

Question

You are given a positive integer n representing the number of nodes of a Directed Acyclic Graph (DAG). The nodes are numbered from 0 to n - 1 (inclusive).

You are also given a 2D integer array edges, where edges[i] = [fromi, toi] denotes that there is a unidirectional edge from fromi to toi in the graph.

Return a list answer, where answer[i] is the list of ancestors of the ith node, sorted in ascending order.

A node u is an ancestor of another node v if u can reach v via a set of edges.

Example 1:

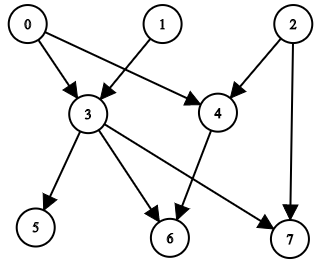
Input: n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6|0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
Output: [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3|],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.

• Nodes 0, 1, and 2 do not have any ancestors.
• Node 3 has two ancestors 0 and 1.
• Node 4 has two ancestors 0 and 2.
• Node 5 has three ancestors 0, 1, and 3.
• Node 6 has five ancestors 0, 1, 2, 3, and 4.
• Node 7 has four ancestors 0, 1, 2, and 3.

Example 2:

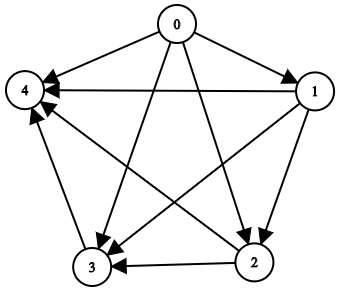
Input: n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4|0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Output: [[],[0],[0,1],[0,1,2],[0,1,2,3|],[0],[0,1],[0,1,2],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.

• Node 0 does not have any ancestor.
• Node 1 has one ancestor 0.
• Node 2 has two ancestors 0 and 1.
• Node 3 has three ancestors 0, 1, and 2.
• Node 4 has four ancestors 0, 1, 2, and 3.

Constraints:

• 1 <= n <= 1000
• 0 <= edges.length <= min(2000, n * (n - 1) / 2)
• edges[i].length == 2
• 0 <= fromi, toi <= n - 1
• fromi != toi
• There are no duplicate edges.
• The graph is directed and acyclic.

Approach 1: Brute Force

Intuition

• For each node, we want all its ancestors (all nodes that can reach it).
• Process nodes in topological order, so when we handle a node curr, we already know all its ancestors.
• Maintain table[child][ancestor] = true.
  • For each edge curr → neighbor:
    • curr is a direct ancestor of neighbor.
    • Every ancestor of curr is also an ancestor of neighbor (transitive propagation).

Algorithm

1. Build graph + indegree
   • Create adjacency list adj from edges.
   • Compute indegree of each node.
2. Topological sort (Kahn)
   • Push all nodes with indegree == 0 into a queue.
3. DP over topo order
   • Initialize table[n][n] = false.
   • While queue not empty:
     • Pop curr.
     • For each neighbor in adj[curr]:
       • Mark direct ancestor: table[neighbor][curr] = true.
       • For all i:
         • If table[curr][i] is true, then table[neighbor][i] = true
           (every ancestor of curr is ancestor of neighbor).
       • Decrease indegree[neighbor]; if it becomes 0, push it.
4. Build answer
   • For each node i:
     • Collect all j where table[i][j] == true into a sorted list answer[i].
   • Return answer.

Code

class Solution {
public:
    vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {
        vector<vector<int>> adj(n, vector<int>());
        vector<int> indegree(n, 0);
        for (int i = 0 ; i < edges.size() ; i++) {
            vector<int> edge = edges[i];
            int u = edge[0];
            int v = edge[1];

            adj[u].push_back(v);
            indegree[v]++;
        }

        queue<int> q;
        for (int i = 0 ; i < n ; i++) {
            if (indegree[i] == 0) {
                q.push(i);
            }
        }

        vector<vector<bool>> table(n, vector<bool>(n, false));

        while(!q.empty()) {
            int curr = q.front();
            q.pop();

            for (auto neighbor: adj[curr]) {
                table[neighbor][curr] = true;
                for (int i = 0 ; i < n ; i++) {
                    if (table[curr][i]) {
                        table[neighbor][i] = true;
                    }
                }

                indegree[neighbor]--;
                if (indegree[neighbor] == 0) {
                    q.push(neighbor);
                }
            }
        }

        vector<vector<int>> answer(n, vector<int>());

        for (int i = 0 ; i < n ; i++) {
            for (int j = 0 ; j < n ; j++) {
                if (table[i][j]) {
                    answer[i].push_back(j);
                }
            }
        }

        return answer;
    }
};

Complexity Analysis

• Time Complexity: $O(N^3)$
• Space Complexity: $O(N^2)$

Related

• 1462. Course Schedule IV