2392. Build a Matrix With Conditions

#leetcode #dsa/graphs

Question

You are given a positive integer k. You are also given:

The two arrays contain integers from 1 to k.

You have to build a k x k matrix that contains each of the numbers from 1 to k exactly once. The remaining cells should have the value 0.

The matrix should also satisfy the following conditions:

Return any matrix that satisfies the conditions. If no answer exists, return an empty matrix.

Example 1:

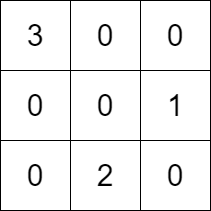
Input: k = 3, rowConditions = [[1,2],[3,2|1,2],[3,2]], colConditions = [[2,1],[3,2|2,1],[3,2]]
Output: [[3,0,0],[0,0,1],[0,2,0|3,0,0],[0,0,1],[0,2,0]]
Explanation: The diagram above shows a valid example of a matrix that satisfies all the conditions.
The row conditions are the following:

Example 2:

Input: k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3|1,2],[2,3],[3,1],[2,3]], colConditions = 2,1
Output: []
Explanation: From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied.
No matrix can satisfy all the conditions, so we return the empty matrix.

Constraints:

Approach 1: Kahn's algorithm (topo sort bfs)

Intuition

Algorithm

  1. Build graph for row conditions and run topological sort.
    If topo is invalid (cycle), return empty matrix.
  2. Build graph for column conditions and run topological sort.
    If topo invalid, return empty matrix.
  3. Create:
    • posRow[x] = position of x in row topo,
    • posCol[x] = position of x in column topo.
  4. Create a k × k matrix filled with 0.
  5. For each number x from 1..k, place it at:
    matrix[posRow[x]][posCol[x]] = x
  6. Return the matrix.

Code

class Solution {
public:
    // Returns a topological ordering of 1..k based on given edges.
    // If it's impossible (cycle), returns an empty vector.
    vector<int> getTopo(vector<vector<int>>& edges, int k) {
        // graph[i] = list of nodes that come after i
        vector<vector<int>> graph(k + 1);
        vector<int> indegree(k + 1, 0);

        for (auto& edge : edges) {
            int from = edge[0];
            int to   = edge[1];
            graph[from].push_back(to);
            indegree[to]++;
        }

        queue<int> q;
        // Nodes are 1..k
        for (int i = 1; i <= k; i++) {
            if (indegree[i] == 0) {
                q.push(i);
            }
        }

        vector<int> topo;
        while (!q.empty()) {
            int node = q.front();
            q.pop();

            topo.push_back(node);

            for (int neighbor : graph[node]) {
                indegree[neighbor]--;
                if (indegree[neighbor] == 0) {
                    q.push(neighbor);
                }
            }
        }

        // If we didn't process all k nodes, there's a cycle → invalid
        if ((int)topo.size() != k) return {};
        return topo;
    }

    vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {
        // Topological orderings for rows and columns
        vector<int> topoRow = getTopo(rowConditions, k);
        vector<int> topoCol = getTopo(colConditions, k);

        // If either is impossible, return empty matrix
        if (topoRow.empty() || topoCol.empty()) return {};

        // posRow[x] = row index of number x
        // posCol[x] = column index of number x
        vector<int> posRow(k + 1), posCol(k + 1);

        for (int i = 0; i < k; i++) {
            posRow[topoRow[i]] = i;
            posCol[topoCol[i]] = i;
        }

        // Build k x k matrix, initially all zeros
        vector<vector<int>> ans(k, vector<int>(k, 0));

        // Place each number 1..k at its (row, col) position
        for (int num = 1; num <= k; num++) {
            int r = posRow[num];
            int c = posCol[num];
            ans[r][c] = num;
        }

        return ans;
    }
};

Complexity Analysis