542. 01 Matrix

• Link: https://leetcode.com/problems/01-matrix/description/

Question

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two cells sharing a common edge is 1.

Example 1:

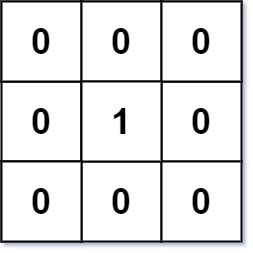
Input: mat = [[0,0,0],[0,1,0],[0,0,0|0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0|0,0,0],[0,1,0],[0,0,0]]

Example 2:

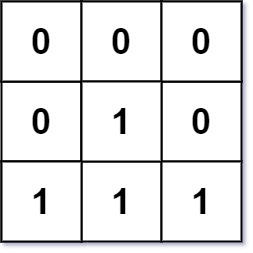
Input: mat = [[0,0,0],[0,1,0],[1,1,1|0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1|0,0,0],[0,1,0],[1,2,1]]

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• There is at least one 0 in mat.

Note: This question is the same as 1765: https://leetcode.com/problems/map-of-highest-peak/

Approach 1: Optimal

Intuition

• Multisource bfs
• Direction array because of grid

Algorithm

1. Initialize an ans matrix initialized with INT_MAX and q
2. Push all the cell pos with the value of 0 in mat
3. BFS on the queue,
   1. If the new distance is less than old distance
      1. change the distance
      2. Push the pos in the queue
4. Return ans;

Code

class Solution {
private:
    const vector<pair<int, int>> directions = {{0, -1}, {-1, 0}, {0, 1}, {1, 0}};
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        int rows = mat.size(), cols = mat[0].size();
        vector<vector<int>> ans(rows, vector<int>(cols, INT_MAX));
        queue<pair<int, int>> q;

        // Initialize the queue with all '0' cells and set their distance to 0 in the answer matrix
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (mat[i][j] == 0) {
                    q.push({i, j});
                    ans[i][j] = 0;
                }
            }
        }

        // Perform multi-source BFS from all '0' cells
        while (!q.empty()) {
            int r = q.front().first;
            int c = q.front().second;
            q.pop();

            for (auto d : directions) {
                int nr = r + d.first;
                int nc = c + d.second;
                if (nr < 0 || nr >= rows || nc < 0 || nc >= cols || ans[nr][nc] <= ans[r][c] + 1) continue;
                ans[nr][nc] = ans[r][c] + 1;
                q.push({nr, nc});
            }
        }

        return ans;
    }
};

Complexity Analysis

• Time Complexity: $O(n\ast m)$
• Space Complexity: $O(n\ast m)$