547. Number of Provinces

#leetcode #dsa/graphs

Question

There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.

A province is a group of directly or indirectly connected cities and no other cities outside of the group.

You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the ith city and the jth city are directly connected, and isConnected[i][j] = 0 otherwise.

Return the total number of provinces.

Example 1:

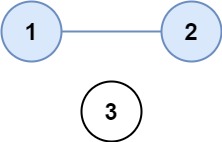
Input: isConnected = [[1,1,0],[1,1,0],[0,0,1|1,1,0],[1,1,0],[0,0,1]]
Output: 2

Example 2:

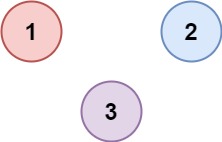
Input: isConnected = [[1,0,0],[0,1,0],[0,0,1|1,0,0],[0,1,0],[0,0,1]]
Output: 3

Constraints:

Approach 1: Optimal Solution

Intuition

Algorithm

  1. Create adjacency list from adjacency matrix
  2. Maintain count of connected components noOfProvinces
  3. Create a visited array
  4. Loop through the visited array and
    1. if a node is not visited then do a traversal through the graph from that point by either dfs or bfs
    2. Increment noOfProvinces
  5. Return noOfProvinces

Code

class Solution {
private:
    void dfs(int node, vector<vector<int>>& adj, vector<int>& visited) {
        if (visited[node]) return;
        visited[node] = 1;
        for (auto neighbor: adj[node]) {
            dfs(neighbor, adj, visited);
        }
    }
	  
    void bfs(int node, vector<vector<int>>& adj, vector<bool>& visited) {
        if (visited[node]) return;

        queue<int> q;
        visited[node] = true; 
        q.push(node);

        while (!q.empty()) {
            int currNode = q.front();
            q.pop();

            for (auto neighbor: adj[currNode]) {
                if (!visited[neighbor]) {
                    visited[neighbor] = true;
                    q.push(neighbor);
                }
            }
        }
    }

    
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        int n = isConnected.size();
        vector<vector<int>> adj(n, vector<int>());
        for (int i = 0 ; i < n ; i++) {
            for (int j = 0 ; j < n ; j++) {
                if (i != j && isConnected[i][j]) {
                adj[i].push_back(j);
                adj[j].push_back(i);
                }
            }
        }

        int noOfProvinces = 0;
        vector<int> visited (n, 0);
				
        for (int i = 0 ; i < n ; i++) {
            if (!visited[i]) {
               noOfProvinces++;
               dfs(i, adj, visited); 
               // bfs(i, adj, visited);
            }
        }

        return noOfProvinces;
    }
};

Complexity Analysis