559. Maximum Depth of N-ary Tree

• Link: https://leetcode.com/problems/maximum-depth-of-n-ary-tree/

Question

Given a n-ary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

Example 1:

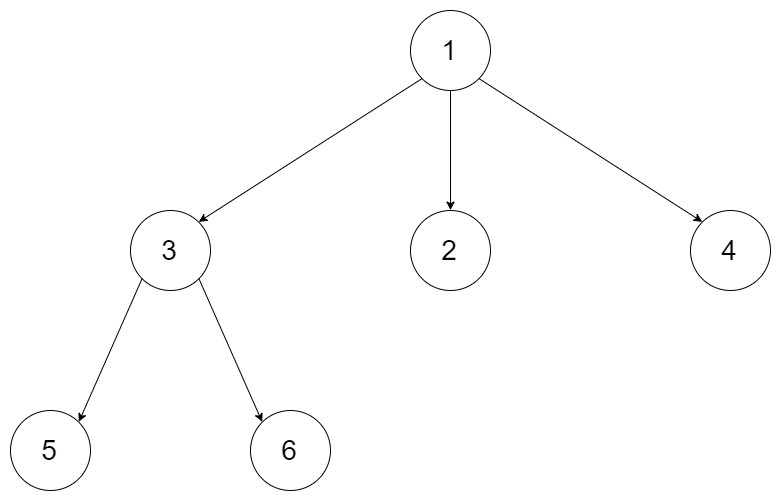
Input: root = [1,null,3,2,4,null,5,6]
Output: 3

Example 2:

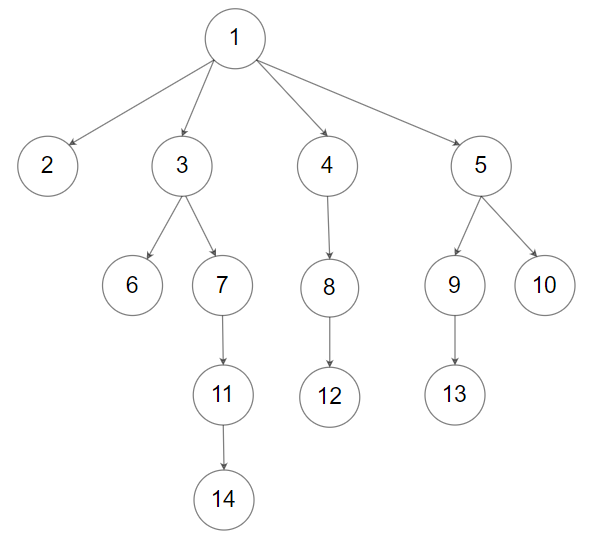
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: 5

Constraints:

• The total number of nodes is in the range [0, 104].
• The depth of the n-ary tree is less than or equal to 1000.

Approach 1: BFS

Intuition

• Tracking depth in BFS is easier and straight forward.

Algorithm

1. Declare and initialize a depth variable with 1 to track the max depth. (1 as if root exists the depth is at least 1)
2. Declare a queue<pair<Node*, int>> to track the depth for each node.
3. Push the root and depth into the queue
4. Loop till queue is not empty
   1. Get the current node and current depth from the front of the queue
   2. Pop the queue
   3. Update the max depth by comparing with the current depth
   4. Loop over the neighbors (children) of the current node
      1. Push them into the queue with currDepth + 1
5. Return depth.

Code

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;
};
*/

class Solution {
public:
    int maxDepth(Node* root) {
        if (root == NULL) return 0;

        int depth = 1;
        // node, depth
        queue<pair<Node*, int>> q;
        q.push({root, 1});    

        while (!q.empty()) {
            Node* node = q.front().first;
            int currDepth = q.front().second;
            q.pop();

            depth = max(currDepth, depth);

            for (auto neighbor: node->children) {
                q.push({neighbor, currDepth + 1});
            }
        }

        return depth;
    }
};

Complexity Analysis

• Time Complexity: $O(N)$
• Space Complexity: $O(N)$

Approach 2: DFS

Intuition

• Traversal option

Algorithm

1. Declare a function getMaxDepth that takes a node and currDepth as argument and returns an int (which is the max depth);
2. We can skip the base case because the tree is going to finish as some point.
3. In the processing & recurse case step we are calling the same function for the children of the node.
4. Calculating the maxDepth by getting the max of the function output of the child and the currentDepth
5. Return the maxDepth

Code

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;
};
*/

class Solution {
public:
    int getMaxDepth(Node* node, int currDepth) {
        int maxDepth = currDepth;
        for (Node* child : node->children) {
            maxDepth = max(best, getMaxDepth(child, currDepth + 1));
        }
        return maxDepth;
    }
    
    int maxDepth(Node* root) {
        if (root == NULL) return 0;

        return getMaxDepth(root, 1);
    }
};

Complexity Analysis

• Time Complexity: $O(N)$
• Space Complexity: $O(N)$