785. Is Graph Bipartite?

• Link: https://leetcode.com/problems/is-graph-bipartite/description/

Question

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

• There are no self-edges (graph[u] does not contain u).
• There are no parallel edges (graph[u] does not contain duplicate values).
• If v is in graph[u], then u is in graph[v] (the graph is undirected).
• The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

Example 1:

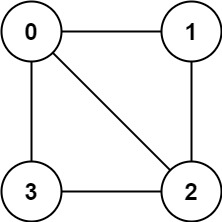
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2|1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2|1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

Constraints:

• graph.length == n
• 1 <= n <= 100
• 0 <= graph[u].length < n
• 0 <= graph[u][i] <= n - 1
• graph[u] does not contain u.
• All the values of graph[u] are unique.
• If graph[u] contains v, then graph[v] contains u.

Approach 1: Optimal

Intuition

• DFS
• Maintaining a color or type array

Algorithm

1. Create n variable for the length of the graph

2. Declare & initialize colors array for storing color for each node of length n initialized to 0

3. Loop through the entire graph adjacency list

   1. if a node is not colored
      1. if dfs of the graph from that node is false
         1. return false

4. return true

5. DFS function

   1. Basecase
      1. if the node is already colored to the same color return true
      2. If the node is colored but not the same color return false
   2. Processing
      1. color the node with the color
      2. decide the next color
   3. Recurse case
      1. for all the neighbors of the node
         1. if dfs for the neighbor with the next color is false
            1. return false
   4. Backtracking
      1. return true

Code

class Solution {
public:
    bool dfs( int node, vector<vector<int>>& graph, vector<int>& colors, int color ) {
        if (colors[node] == color) return true;
        if (colors[node]) return false;
        colors[node] = color;

        int nextColor;
            
        if (color == 1) {
            nextColor = 2;
        } else {
            nextColor = 1;
        }

        for (int neighbor: graph[node]) {
            if (!dfs(neighbor, graph, colors, nextColor)) {
                return false;
            }
        }
        return true;
    }
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        vector<int> colors(n, 0);

        for (int i = 0 ; i < n ; i++) {
            if (!colors[i]) {
                if(!dfs(i, graph, colors, 1)) {
                    return false;
                };
            }
        }

        return true;
    }
};

Complexity Analysis

• Time Complexity: $O(n+2e)$
• Space Complexity: $O(n)$
  • Where
    • n -> node
    • e -> edge