802. Find Eventual Safe States

• Link: https://leetcode.com/problems/find-eventual-safe-states/description/

Question

There is a directed graph of n nodes with each node labeled from 0 to n - 1. The graph is represented by a 0-indexed 2D integer array graph where graph[i] is an integer array of nodes adjacent to node i, meaning there is an edge from node i to each node in graph[i].

A node is a terminal node if there are no outgoing edges. A node is a safe node if every possible path starting from that node leads to a terminal node (or another safe node).

Return an array containing all the safe nodes of the graph. The answer should be sorted in ascending order.

Example 1:

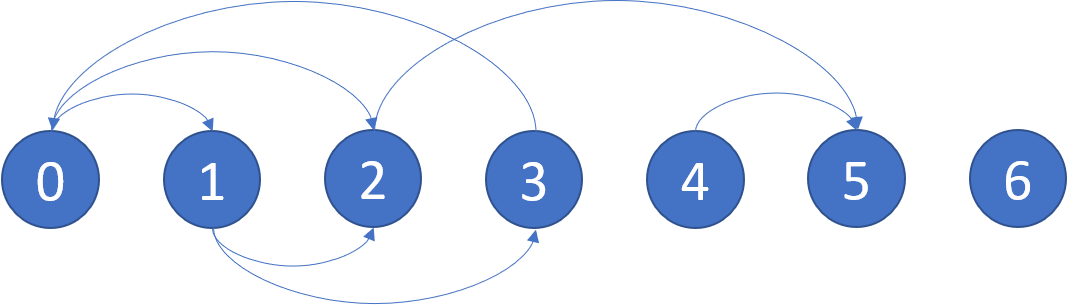
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[|1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Explanation: The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.

Example 2:

Input: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[|1,2,3,4],[1,2],[3,4],[0,4],[]]
Output: [4]
Explanation:
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.

Constraints:

• n == graph.length
• 1 <= n <= 104
• 0 <= graph[i].length <= n
• 0 <= graph[i][j] <= n - 1
• graph[i] is sorted in a strictly increasing order.
• The graph may contain self-loops.
• The number of edges in the graph will be in the range [1, 4 * 104].

Approach 1: DFS

Intuition

• Cycle detection

Algorithm

1. Declare & initialize 3 arrays visited, pathVisited, safeStates with size n & value 0
2. Loop through the graph and if the node is not visited call dfs for that node
3. Declare vector<int> ans
4. Iterate through safeStates vector
   1. If safeStates for a node is equal to 1
      1. Push that node into the ans vector
5. Return ans

• DFS
  1. Base Case
     1. If visited & path visited
        1. Set not a safe state (as cycle detected)
        2. Return true
     2. If visited & not pathVisited
        1. Set as a safe state (as cycle not detected)
        2. Return false
  2. Processing
     1. Set visited
     2. Set pathVisited
  3. Recurse Case
     1. Iterate through the neighbors of the node in the graph
     2. Call dfs for each neighbor, if it returns true
        1. Set safeStates for the Current Node = 0
        2. Return true
  4. Back tracking
     1. Set safeStates for the Current Node = 1
     2. Reset pathVisited for the node
     3. Return false;

Code

class Solution {
public:
    bool dfs(int node, vector<vector<int>>& graph, vector<int>& visited,
             vector<int>& pathVisited, vector<int>& safeStates) {
				// base case
        if (visited[node] && pathVisited[node]) {
            safeStates[node] = 0;
            return true;
        }
        if (visited[node] && !pathVisited[node]) {
            safeStates[node] = 1;
            return false;
        }

				// processing
        visited[node] = 1;
        pathVisited[node] = 1;

				// recurse case
        for (auto neighbor : graph[node]) {
            if (dfs(neighbor, graph, visited, pathVisited, safeStates)) {
                safeStates[node] = 0;
                return true;
            }
        }

				// backtracking
        safeStates[node] = 1;
        pathVisited[node] = 0;
        return false;
    }
    vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
        int n = graph.size();
        vector<int> visited(n, 0);
        vector<int> pathVisited(n, 0);
        vector<int> safeStates(n, 0);

        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                dfs(i, graph, visited, pathVisited, safeStates);
            }
        }

        vector<int> ans;
        for (int i = 0; i < n; i++) {
            if (safeStates[i] == 1) {
                ans.push_back(i);
            }
        }

        return ans;
    }
};

Complexity Analysis

• Time Complexity: $O(V+E)$
• Space Complexity: $O(V+E)$

Approach 2: BFS (Kahn's Algorithm)

Intuition

• TOPO sort
• Kahn's Algorithm

Algorithm

1. Initialize variables:
   • n = number of nodes in the graph
   • revGraph: a new graph to store the reversed edges
   • indegree: an array to count incoming edges in the reversed graph
   • queue: for BFS traversal of safe nodes
   • safeStates: a list to store the final answer
2. Build the reversed graph:
   • For each edge i → neighbor in graph:
     • Add an edge neighbor → i in revGraph
3. Compute indegrees in the reversed graph:
   • For every node i, iterate over revGraph[i]:
     • Increment indegree[neighbor]++
4. Push nodes with 0 indegree into the queue:
   • These nodes have no outgoing edges in the original graph, so they are safe
5. Run BFS (Kahn’s Algorithm):
   • While queue is not empty:
     • Pop a node node
     • Add node to safeStates
     • For each neighbor in revGraph[node]:
       • Decrease indegree[neighbor]--
       • If indegree[neighbor] == 0, push neighbor into the queue
6. Sort safeStates (optional depending on output requirement)
7. **Return safeStates

Code

class Solution {
public:
    vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
        int n = graph.size();
        vector<vector<int>> revGraph(n, vector<int>());

        for (int i = 0 ; i < n ; i++) {
            for (auto neighbor: graph[i]) {
                revGraph[neighbor].push_back(i);
            }
        }

        vector<int> indegree(n, 0);

        for (int i = 0 ; i < n ; i++) {
            for (int neighbor: revGraph[i]) {
                indegree[neighbor]++;
            }
        }

        queue<int> q;

        for (int i = 0 ; i < n ; i++) {
            if (indegree[i] == 0) {
                q.push(i);
            }
        }

        vector<int> safeStates;

        while (!q.empty()) {
            int node = q.front();
            q.pop();
            safeStates.push_back(node);

            for (int neighbor: revGraph[node]) {
                indegree[neighbor]--;
                if (indegree[neighbor] == 0 ) {
                    q.push(neighbor);
                }
            }
        }

        sort(safeStates.begin(), safeStates.end());

        return safeStates;
    }
};

Complexity Analysis

• Time Complexity: $O(V+E)$
• Space Complexity: $O(V+E)$