Directed Graph Cycle GFG

• Link: https://www.geeksforgeeks.org/problems/detect-cycle-in-a-directed-graph/1?itm_source=geeksforgeeks&itm_medium=article&itm_campaign=practice_card

Question

Given a Directed Graph with V vertices (Numbered from 0 to V-1) and E edges, check whether it contains any cycle or not.
The graph is represented as a 2D vector edges[][], where each entry edges[i] = [u, v] denotes an edge from verticex u to v.

Examples:

Input: V = 4, edges[][] = 0, 1], [0, 2], [1, 2], [2, 0], [2, 3

Output: true
Explanation: The diagram clearly shows a cycle 0 → 2 → 0

Input: V = 4, edges[][] = [[0, 1], [0, 2], [1, 2], [2, 3]

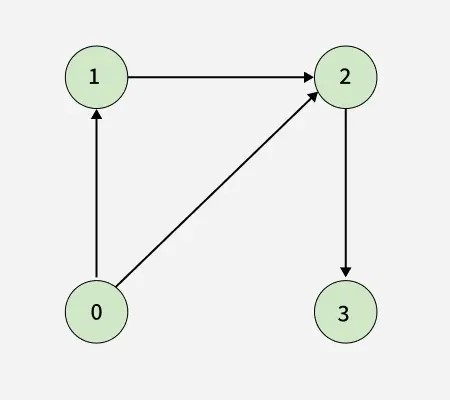
Output: false
Explanation: no cycle in the graph

Constraints:
1 ≤ V, E ≤ 105

Try more examples

Approach 1: DFS

Intuition

• DFS
• Visited array
• Path visited array to maintain the current path

Algorithm

1. Coveted edge list to adjacency list
2. Create visited array & pathVisited array of length V.
3. For covering connected components loop through the visited array
   1. If not visited then
      1. Call dfs for the node
      2. If it returns true then return true.
4. return false;

• BFS
  1. Base case
     1. If node is visited & pathVisited then cycle exists return true
     2. If node is visited but not pathVisited then cycle doesn't exist return false
  2. Processing
     1. Mark visited & path visited
  3. Recurse case
     1. Call dfs for all the neighbors if true then return true
  4. Back tracking
     1. Reset pathVisited to 0
     2. return false;

Code

class Solution {
public:
    vector<vector<int>> getAdj(int V, vector<vector<int>>& edges) {

        vector<vector<int>> adj(V, vector<int>() );

        for (auto edge: edges) {
            int startNode = edge[0];
            int endNode = edge[1];
            adj[startNode].push_back(endNode);
        }

        return adj;
    }

    bool dfs(int node, vector<vector<int>>& adj, vector<int>& visited, vector<int>& pathVisited) {
        // Base case
        if (visited[node] && pathVisited[node]) return true;
        if (visited[node] && !pathVisited[node]) return false;

        // Processing / Business logic
        visited[node] = 1;
        pathVisited[node] = 1;

        // Recurse case
        for (int neighbor : adj[node]) {
            if (dfs(neighbor, adj, visited, pathVisited)) return true;
        }

        // Backtracking
        pathVisited[node] = 0;
        return false;
    }

    bool isCyclic(int V, vector<vector<int>> &edges) {

        vector<vector<int>> adj = getAdj(V, edges);

        vector<int> visited(V, 0);
        vector<int> pathVisited(V, 0);

        for (int i = 0 ; i < V ; i++) {
            if (!visited[i]) {
                if (dfs(i, adj, visited, pathVisited)) return true;
            }
        }

        return false;
    }
};

Complexity Analysis

• Time Complexity: $O(V+E)$
• Space Complexity: $O(V+E)$
• Where,
  • V = no. of nodes
  • E = no. of edges

Approach 2: BFS (Topological sort - Kahn's Algorithm GFG)

Intuition

• BFS
• Topo sort is only applicable for DAG (Directed Acyclic Graph)
• If we are not able to generate a valid topo sort it means the we have a Cyclic graph
• We can use Kahn's algorithm to type to get the topo sort If the length is not equal to the total no. of nodes then the graph is cyclic

Algorithm

1. Get adjacency list from edge list
2. Declare & initialize vector<int> indegree with length of the nodes & zero
3. Update the indegree by looping through the adjacency list
4. Declare a queue<int> q
5. Loop through the indegree array
   1. If the indegree of a node == 0 then push it into the queue
6. Declare an vector<int> ans array
7. While q is not empty
   1. Get the node at the front of the queue & pop it
   2. Push the node into the q
   3. Loop over the neighbors of the node
      1. Decrement the indegree by 1
      2. If the indegree == 0 then push it into the queue
8. if ans length is equal to total no. of nodes then return false
9. else return true.

Code

class Solution {
public:
    vector<vector<int>> getAdj(int V, vector<vector<int>>& edges) {
        vector<vector<int>> adj(V);
        for (auto edge : edges) {
            adj[edge[0]].push_back(edge[1]);
        }
        return adj;
    }


    bool isCyclic(int V, vector<vector<int>> &edges) {
        vector<vector<int>> adj = getAdj(V, edges);

        vector<int> indegree (V, 0);

        for (int i = 0 ; i < V ; i++) {
            for (int neighbor: adj[i]) {
                indegree[neighbor]++;
            }
        }

        queue<int> q;

        for (int i = 0 ; i < V ; i++) {
            if (indegree[i] == 0) {
                q.push(i);
            }
        }

        vector<int> ans;

        while (!q.empty()) {
            int node = q.front();
            q.pop();
            ans.push_back(node);

            for (int neighbor: adj[node]) {
                indegree[neighbor]--;

                if (indegree[neighbor] == 0) {
                    q.push(neighbor);
                }
            }
        }

        if (ans.size() == V) return false;
        return true;
    }
};

Complexity Analysis

• Time Complexity: $O(V+E)$
• Space Complexity: $O(V+E)$
• Where,
  • V = no. of nodes
  • E = no. of edges