Find length of Loop GFG

• Link: https://www.geeksforgeeks.org/problems/find-length-of-loop/1

Question

Given the head of a linked list, determine whether the list contains a loop. If a loop is present, return the number of nodes in the loop, otherwise return 0.

Note: 'c' is the position of the node which is the next pointer of the last node of the linkedlist. If c is 0, then there is no loop.

Examples:

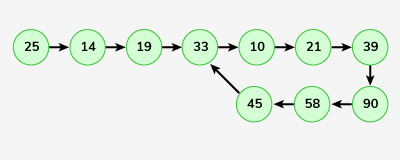
Input: LinkedList: 25->14->19->33->10->21->39->90->58->45, c = 4
Output: 7
Explanation: The loop is from 33 to 45. So length of loop is 33->10->21->39-> 90->58->45 = 7. The number 33 is connected to the last node of the linkedlist to form the loop because according to the input the 4th node from the beginning(1 based indexing)
will be connected to the last node for the loop.

Input: LinkedList: 5->4, c = 0
Output: 0
Explanation: There is no loop.

Expected Time Complexity: O(n)
Expected Auxiliary Space: O(1)

Constraints:
1 <= no. of nodes <= 106
0 <= node.data <=106
0 <= c<= n-1

Try more examples

Approach 1: Brute Force

Intuition

• Using hashing with unordered_map data structure.

Algorithm

1. Declare an unordered_map<Node*, int> m
2. Declare & initialize count = 1
3. Declare & initialize Node* curr to head
4. Loop through the LL using the curr node.
   1. If curr node exists in the map m
      1. Return count - m[curr], length of the loop
   2. Add curr to the map m with the value of count.
   3. Increment count by 1
   4. curr = curr->next
5. Return 0, meaning there is no loop.

Code

class Solution {
  public:
    // Function to find the length of a loop in the linked list.
    int countNodesinLoop(Node *head) {
		
        unordered_map<Node*, int> m;
        int count = 1;
        Node* curr = head;
        
        while (curr) {
            if (m.find(curr) != m.end()) {
                return count - m[curr];
            }
            m[curr] = count;
            count++;
            curr = curr->next;
        }
        
        return 0;
    }
};

Complexity Analysis

• Time Complexity: $O(N)$
• Space Complexity: $O(N)$

Approach 2: Optimal

Intuition

• Floyd's tortoise hare cycle detection algorithm.

Algorithm

1. Declare & initialize Node* fast & Node* slow to head;
2. Loop through the LL till fast != NULL && fast->next != NULL
   1. fast = fast->next->next fast moves with 2 nodes at a time.
   2. slow = slow->next slow moves with 1 node at a time.
   3. if fast == slow
      1. Declare & initialize a int count = 1
      2. fast = fast->next
      3. loop through the LL again till fast != slow
         1. fast = fast->next increment fast by 1.
         2. count++
      4. Return count
3. Return 0;

Code

class Solution {
  public:
    // Function to find the length of a loop in the linked list.
    int countNodesinLoop(Node *head) {
        
        Node* fast = head;
        Node* slow = head;
        
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
            
            if (fast == slow) {
                int count = 1;
                fast = fast->next;
                while (fast != slow) {
                    fast = fast->next;
                    count++;
                }
                return count;
            }
        }
        
        return 0;
    }
};

Complexity Analysis

• Time Complexity: $O(N)$
• Space Complexity: $O(1)$